The choice of shot quiz

Do better players make better decisions? Of course they do. But can we show that to be true, can we prove it? After all, there are personal preferences, even amongst the top players. They love some shots, and avoid others. So if top player A and top player B sometimes have a different first choice, we would need to know their second, third and fourth preference to establish a pattern. If it's there, we can at least make a difference between the superior and the inferior solutions.

Are you a 0.500 player because you play the right shots? In other words, you would be a 0.400 if you were not so clever. Or are you a 0.500 player because you play the WRONG shots? In other words, you could be a 0.600 if you got smarter.

Facebook is the perfect place to ask a question to many people. I used the Dutch billiard page started by Paul Brekelmans (and what a wonderful service for players he provides) as well as my own, Bert's Billiard Page. Within two days, more than 300 people responded. Thank you all for being so helpful.  

This was the question:  

If the balls were placed like this, which solution would be your first, second, third and fourth choice to play? It's not about playing for position, this is your last point.

I drew the diagram in such a way, that all 5th, 6th and other solutions would be inferior to the four choices presented. They are beside the point anyway; what mattered to me was the question: will the preferences of players change towards the better solutions as their average goes up?  

Yes, there are good solutions: B and A, in that order. And lesser ones: D and C. I was quite convinced that a small panel of expert players would confirm that, and I would only have to look at the amount of A's and B's to see the quality of choice. To my surprise, I was only partially right. I did get the expert vote I wanted and expected: BADC, but more people liked option D than I had foreseen, even amongst stronger players. Let me walk you through the four diagrams. 

Solution A. 

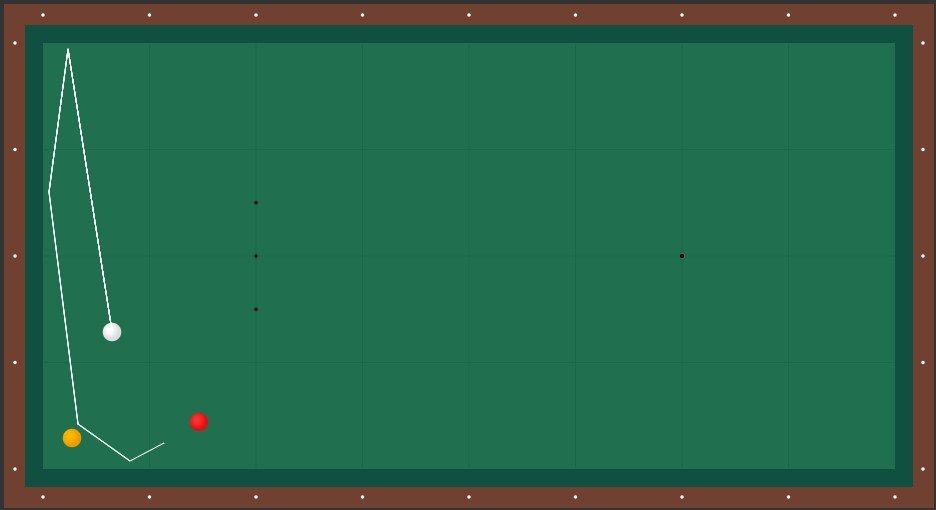
Normally, you avoid playing cushion first. And two-rails first is (quite often) even more difficult than three-rails first. But in this case, the balls are set up perfectly for the shot. The yellow is roughly a ball away from both rails. If that was, for example, only one third of a ball, it would often cause a double kiss when hit, with unpredictable results. The red ball is a natural target off yellow and long rail: you can't go around it and only with a hit that is very thin will you miss it inside. This, in conclusion, is an easy shot. Roll your ball into the right half of the yellow, some helping english will develop automatically and you'll have a big margin for error. 

Solution B.

Choice of shot is always in the details. For this one, the deciding factor is the distance between the yellow ball and the short rail. It's about one ball away, which is quite generous. Play the little draw shot: red - long - long - short and you will be aiming at a very "big ball". Don't use right hand english on this shot, it will straighten up your ball after the second rail and you will have shrunk your target (considerably).  If the distance between the yellow and the short rail had been one-third of a ball or less, the good players would have looked long and hard at other solutions. In the situation of the diagram, they instantly recognized it as an easy point.    

Solution C.

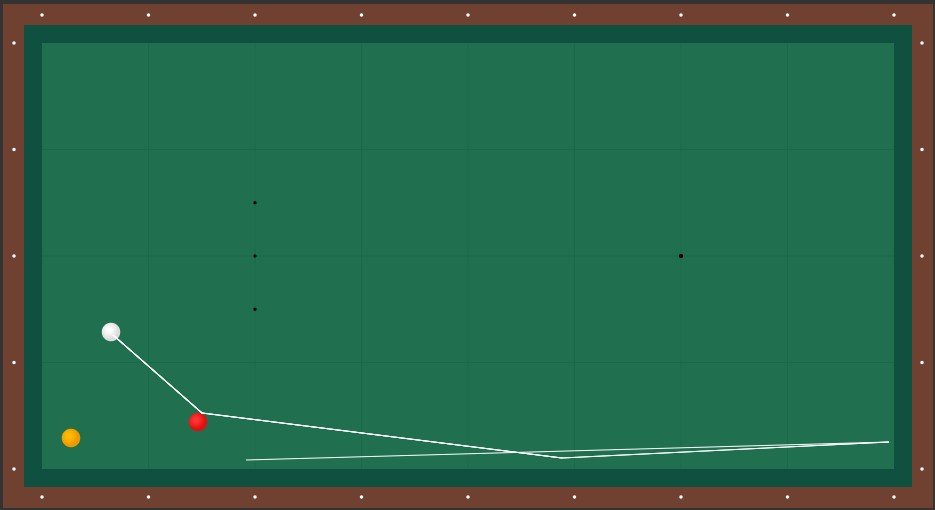
Quite obviously the toughest of the four, so the one you should NOT have picked as your first choice. The cue ball needs to travel far, and the amount of english in the shot must correspond perfectly with the amount of object ball you hit. Sure, the good players will make this more often than they will miss, but they avoid it with good reason. Is this shot easier if you hit a thinner second ball and use maximum english? Not in my experience. The amount of "bite" on the second (short) rail can seriously differ from table to table. 

Solution D.   

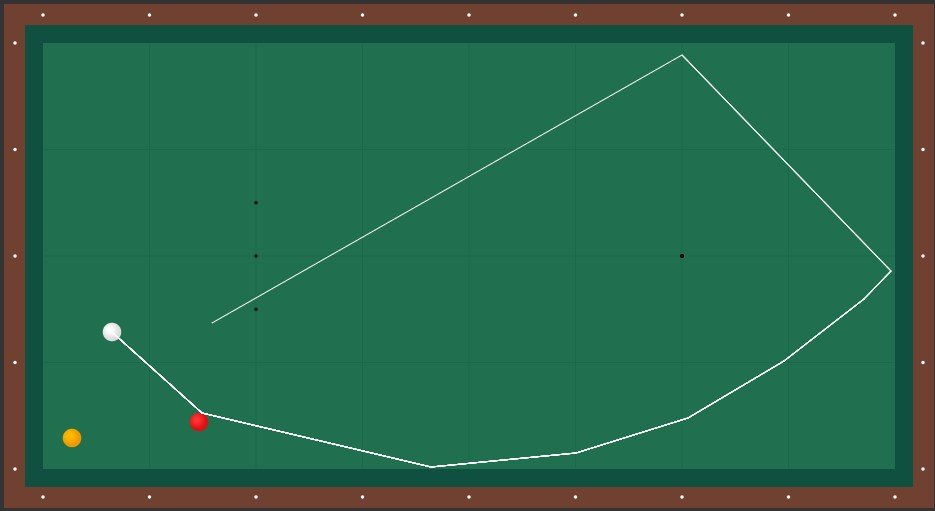
How can I say this without stepping on anybody's toes? I think many people have not looked at the (crude) diagram long and hard enough.  Especially in the V, W and X brackets, some must have thought it was a natural, a thin hit off the red, around the table to a (very) big ball in the corner. But the shot is set up in such a way that the thin hit is not available. Even on older cloth, you would need a hit so thin that the red hardly moves, to have a chance. On newer, sliding cloth, you have NO chance. To make the D - shot, you need to curve the ball in, with draw. A surprising number of people selected this option as their first, and I think many of them would have all sorts of problems executing it correctly. You can't hit a wafer-thin second ball with lots of draw: you'll be short. You can't hit the second ball a quarter full: you'll be long. This is a demanding shot that requires knowledge, some "feel" and more technique than most under 0.6 players have at their disposal.   

The expert group consisted of Eddy Leppens, Jean van Erp, Jef Philipoom, Dave Christiani, Raymond Ceulemans, Roland Forthomme, Peter Ceulemans and Murat Naci Coklu. All of them extremely good players, and none of them are known for frivolous decisions. Together, they voted  BADC. Or rather, that was the sum total, with small positives for B, A, and D (in that order), and a big negative for C.  If I award 2 points for a first choice, 1 point for a second choice, -1 for a third and -2 for a fourth, the net result is B +6, A+5, D +3, C -14. The fact that the "professional" result spells "Bad C" is a little joke I couldn't resist.    

Group V consisted of players who volunteered  to say they average below 0.350 (and a few referees, whose opinions are always valuable). There were 18 votes in V, and they resulted in A -25, B +14, C -12 and D + 23. 

Group W had 85 votes, from people who average 0.350 - 0.499. It was - of course - impossible for me to check all these people's actual playing strength, so we'll just have to take their word for it. They voted as follows: A -52, B +41, C -46, D +57. 

Group X had 77 votes, in the 0.500 - 0.649 bracket. They rejected A as much as the W group did, which came as a surprise. I expected the appreciation for A to go up, with the over-0.500's. A was -51, B +59, C -30 and D + 22.

In group Y we find 55 pretty good players, who estimate themselves to be between 0.650 and 0.799. They voted as follows: A -38, B +34, C -33 and D +37. So there is very little difference between the X and the Y players.

The Z category starts at 0.800, and they gave us 32 votes. A 0, B +32, C -45 and D +13. This is where a big shift takes place: the negative assessment of the bank shot (A) is gone, and people start to see the relative difficulty of shot D.     

An improvised category was added by me, because it proved to be rather easy to identify the over 1.000 average players. So I gave them their own bracket, ZZ. We had 15 votes there, so you could say that the V category was under the field and the ZZ was above it. The ZZ's voted A -4, B +22, C -18 and D 0.  Just to remind you: one step further up was the expert group, and they voted A +5, B +6, C -14 and D +3.  

Roughly 20 votes were incomplete or otherwise unusable.   

What are the conclusions I can come up with from these results?   

- There was little or no controversy about shots B and C, in all the field. B is a good shot, C is not so good. This quiz turned out to be mostly about shots A and D. For D, the task was to recognize how - relatively - difficult it was, for A, the task was to recognize how - relatively - easy it was. The better the players, the more they saw it.

- The decisions made by players who are roughly 0.575 are not dramatically different from those made by players who are roughly 0.425. That leads me to believe that stance & stroke, technique, hitting a ball well is the main thing that separates a 0.400 from a 0.500 and a 0.500 from a 0.600. They will play the vast majority of shots the same way, but not with the same quality.

- Experts do not necessarily agree. If I ever do a survey of this type again, I will use a larger "control group". In a group of only 8, a single dissenting vote can have too much impact. 

- Can we explain the preference for D amongst players with a lower average by saying: "they just didn't see on the diagram that it was not a simple thin hit round the table off the red"? Well, that is actually the point, isn't it? Seeing these things makes you a better player. Obviously, you will get a better view at the table than looking at a diagram, I realize that. But Dani will show Tayfun a position using finger gestures on the back of a smartphone, and the Turk will recognize the kiss that comes into play after five rails! There is a world of knowledge and quick perception that separates the W's from the experts.   

- Choice of shot is, or should be, about chance of success. Getting to know the percentages is crucial. When faced with a choice between two very makeable shots, the expert will instantly ask himself: "which one will give me the best chance of position?". When faced with two shots that are difficult, the strong player will always pick the 13 % shot over the 6 % shot. To the amateur, they can look the same: desperately difficult. But the pro knows the difference.  

- Everything about billiards is in the details. If I move one of the three balls in the starting diagram an inch and a half, every vote and expert opinion goes out the window, and we can start from scratch. Which is exactly what you need to do when you play a game of 3-cushion: look at every position as if it is slightly different from the thousands of similar ones you have seen before in your life. Because it is.   

- Finally, there is the matter of reading diagrams. It is very easy to get a wrong idea, when your view of the problem has been reduced in size from 284 cm to 8 cm.  I am positive that a good percentage of the first choice D voters would have reconsidered, had they been standing next to an actual billiard table with this position set up. Also, in that live situation, with a billiard you can walk around, there would most certainly have been more agreement amongst the eight top players.